집합의 정의 및 표기법

\[A = \{\{1,2,3,4,5\}\}\] \[B = \{\{a,b,c,d\}\}\]

대수학을 이해하는 데 있어 기본적이고 중요한 개념 중 하나는 ‘집합(Set)’이다. 이 글에서는 집합이 무엇인지와 집합을 표현하는 다양한 방법에 대해 알아보자

집합이란?

• 명확히 정의되고 구별 가능한 객체들의 모임
  • 이 객체들을 ‘원소(Elements)’라고 부른다.
• 집합은 수학적 개념뿐만 아니라 일상생활에서도 흔히 접할 수 있는 개념이다.

집합의 표기법 (Notations)

• 집합을 표현하는 방법에는 여러 가지가 있다. 가장 일반적인 방법은 원소 나열법, 조건 제시법, 벤 다이어그램이다.

원소 나열법 (Enumerating Elements, Roster Form)

• 집합을 이루는 원소들을 나열하여 표현하는 방법
• 집합의 원소를 순서에 상관없이 중괄호 { } 안에 나열하는 방법이다
• 원소의 순서는 중요하지 않으며, 중복되지 않게 원소는 한 번만 나열한다.

• 숫자의 집합 : \(A = \{\{1,2,3,4,5\}\}\)
• 문자의 집합 : \(B = \{\{a,b,c,d\}\}\)
• 혼합된 원소의 집합 : \(C = \{\{red,1,true,\pi \}\}\)

조건 제시법 (Set Builder)

• 집합의 원소들이 만족해야 하는 특정 조건을 기술하여 집합을 정의한다.
• 일반적으로 { } 안에 원소를 나타내는 변수와 그 변수에 적용되는 조건을 기록한다.
  • 변수와 조건은 | 로 구분지어 기록한다
• 원소들이 만족해야 하는 조건을 명확하게 기술해야 한다.
• 더 복잡하고 추상적인 집합을 정의할 때 유용하다.

• 짝수의 집합 : \(A = \{\{ x \lvert x는 짝수 \}\}\)
• 특정 조건을 만족하는 집합 : \(B = \{\{ y \lvert y > 0, y는 실수 \}\}\)
• 함수의 범위를 나타내는 집합 : \(C = \{\{ z \lvert z = x^{2}, 0 \leq x \leq 5 \}\}\)

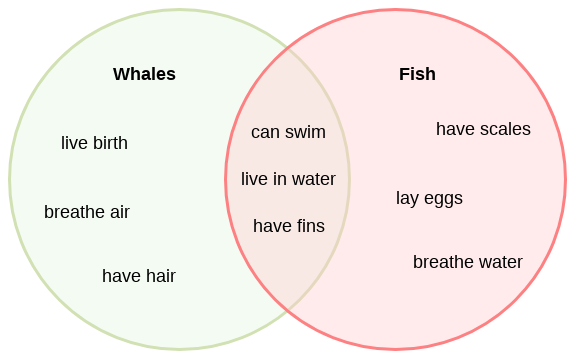
벤 다이어그램 (Venn Diagram)

• 집합과 집합 간의 관계를 시각적으로 나타내는 방법이다
  • 시각적으로 나타내므로, 교집합, 합집합, 차집합 등 집합 간의 관계를 이해하는 데 도움을 준다.
• 원을 사용하여 각 집합을 표현하고, 이들의 교차 부분으로 집합 간의 관계를 나타낸다.

수학적 집합과 그 표현

전체 집합 (Universal Set)

• 기호: \(U\) 또는 \(S\)
• 특정 상황 또는 문맥에서 고려되는 모든 가능한 원소를 포함하는 집합

공집합 (Empty Set)

• 기호: \(\phi\) 또는 \(\{\{ \}\}\)
• 원소가 전혀 없는 집합으로 집합 간의 연산에서 ‘없음’ 또는 ‘빈 경우’를 나타내는 집합

• 두 집합 \(A = \{\{1,2,3 \}\}\) 와 \(B = \{\{4,5,6 \}\}\)의 교집합 : \(A \cap B = \phi\)
• 어떤 조건을 만족하는 원소가 없는 경우 : \(\{\{ x \lvert x < 0, x는 자연수 \}\} = \phi\)

자연수 (Natural Numbers)

• 기호: \(\mathbb{N}\)

\[\mathbb{N} = \{1, 2, 3, \ldots\}\]

전체수 (Whole Numbers)

• 기호: \(\mathbb{W}\)
• 자연수에 0을 포함한 집합

\[\{0, 1, 2, \ldots\}\]

정수 (Integers)

• 기호: \(\mathbb{Z}\)

\[\mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}\]

유리수 (Rational Numbers)

• 기호: \(\mathbb{Q}\)
• 분수 형태로 표현되는 모든 수들의 집합

\[\mathbb{Q} = \{\{ \frac{p}{q} | p, q \in \mathbb{Z}, q \neq 0 \}\}\]

무리수 (Irrational Numbers)

• 기호: \(\mathbb{I}\)
• 유리수로 표현될 수 없는 수들의 집합

\[\{x | x \text{는 무리수}\}\]

실수 (Real Numbers)

• 기호: \(\mathbb{R}\)
• 모든 유리수와 무리수를 포함하는 집합

\[\mathbb{R} = \{x | x \text{는 유리수 또는 무리수}\}\]

복소수 (Complex Numbers)

• 기호: \(\mathbb{C}\)
• 실수와 허수를 모두 포함하는 집합

\[\mathbb{C} = \{a + bi | a, b \in \mathbb{R}, i = \sqrt{-1}\}\]

집합으로 표현되는 함수와 공간

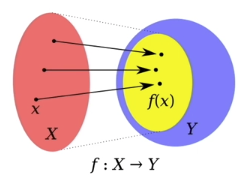
함수

• 집합은 함수는 입력과 출력의 관계를 정립하는 데 사용될 수 있다

직선과 평면

• 기하학적 공간에서의 위치와 형태를 정의하는 직선과 평면 등을 표현하는데도 사용할 수 있다

\[L = \{(x,y) | y = ax + b\}\]

\[P = \{(x,y,z) | n \cdot (r - r_0) = 0\}\]

방정식과 부등식의 해집합

• 방정식과 부등식의 해를 집합으로 표현할 수 있다

\[S = \{x | f(x) = 0\}\]

\[S = \{x | f(x) < 0\}\]

좌표 공간

• 물리적 또는 추상적 공간에서의 위치와 다차원 공간을 나타내는 데 사용될 수 있다

\[\mathbb{R}^2 = \{(x,y)\}\]

\[\mathbb{R}^3 = \{(x,y,z)\}\]

\[\mathbb{R}^n = \{(x_1, x_2, \ldots, x_n)\}\]